SSC CGL 2023- Important Quant Topics (Triangle)

In SSC CGL exam, several questions are asked in Geometry. In this article, we will run you through several concepts related to Geometry along with examples so that you can understand them easily. Let’s get started.

Incircle of a triangle

An incircle is a circle that is tangent to all three sides of a triangle. The center of the incircle is called the incenter. The incenter can be found by intersecting the angle bisectors of the triangle.

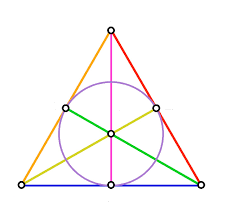
The inradius is the radius of the incircle. The inradius can be found by dividing the area of the triangle by the semiperimeter of the triangle.

The incircle has several properties, including:

• The inradius is equal to the ratio of the area of the triangle to the semiperimeter of the triangle.
• The incenter is equidistant from the three sides of the triangle.
• The incircle is tangent to the three sides of the triangle at the midpoints of the sides.
• The incircle is tangent to the nine-point circle of the triangle.

The incircle can be used to solve a variety of problems involving triangles, such as finding the area of the triangle, finding the length of a side of the triangle, or finding the distance between two points on a side of the triangle.

Inradius of a triangle

An inradius is the radius of a circle that is tangent to all three sides of a triangle. The inradius is denoted by r.

The inradius can be found using the following formula:

r = S / s

where S is the area of the triangle and s is the semiperimeter of the triangle.

The inradius has several properties, including:

• The inradius is equal to the ratio of the area of the triangle to the semiperimeter of the triangle.
• The incenter is equidistant from the three sides of the triangle.
• The incircle is tangent to the three sides of the triangle at the midpoints of the sides.
• The incircle is tangent to the nine-point circle of the triangle.

The inradius can be used to solve a variety of problems involving triangles, such as finding the area of the triangle, finding the length of a side of the triangle, or finding the distance between two points on a side of the triangle.

Here is an example of how to use the inradius to find the area of a triangle:

Given: A triangle with sides of length 3, 4, and 5.

To find: The area of the triangle.

Solution:

1. Find the semiperimeter of the triangle: s = (3 + 4 + 5) / 2 = 6

2. Find the area of the triangle: S = r * s = (6 * 3) / 2 = 9

Therefore, the area of the triangle is 9.

Circumcenter of a Triangle

The circumcenter of a triangle is the center of the circle that passes through all three vertices of the triangle. The circumcenter is denoted by O.

The circumcenter can be found by intersecting the perpendicular bisectors of the sides of the triangle.

The circumcenter has several properties, including:

• The circumcenter is equidistant from the three vertices of the triangle.
• The circumradius is equal to the distance between the circumcenter and any vertex of the triangle.
• The circumcircle is tangent to the three sides of the triangle at the midpoints of the sides.

The circumcenter can be used to solve a variety of problems involving triangles, such as finding the area of the triangle, finding the length of a side of the triangle, or finding the distance between two points on a side of the triangle.

Here is an example of how to use the circumcenter to find the area of a triangle:

Given: A triangle with vertices A, B, and C.

To find: The area of the triangle.

Solution:

1. Find the circumcenter of the triangle: O

2. Find the radius of the circumcircle: r = OA = OB = OC

3. Find the area of the triangle: S = r * s = r * (AB + BC + CA) / 2

Therefore, the area of the triangle is S.

Circumradius of a Triangle

The circumradius of a triangle is the radius of the circle that passes through all three vertices of the triangle. It is denoted by R.

The circumradius can be found using the following formula:

R = 2S / (a + b + c)

where S is the area of the triangle and a, b, and c are the lengths of the sides of the triangle.

The circumradius has several properties, including:

• The circumradius is equal to the product of the semiperimeter of the triangle and the inradius.
• The circumradius is equal to the distance between the circumcenter and any vertex of the triangle.
• The circumcircle is tangent to the three sides of the triangle at the midpoints of the sides.

The circumradius can be used to solve a variety of problems involving triangles, such as finding the area of the triangle, finding the length of a side of the triangle, or finding the distance between two points on a side of the triangle.

Here is an example of how to use the circumradius to find the area of a triangle:

Given: A triangle with sides of length 3, 4, and 5.

To find: The area of the triangle.

Solution:

1. Find the semiperimeter of the triangle: s = (3 + 4 + 5) / 2 = 6

2. Find the inradius: r = S / s = (6 * 3) / 2 = 9

3. Find the circumradius: R = 2S / (a + b + c) = 2 * 9 / (3 + 4 + 5) = 6

4. Find the area of the triangle: S = r * R = 9 * 6 = 54

Therefore, the area of the triangle is 54.

Orthocenter of a Triangle

The orthocenter of a triangle is the point of intersection of the altitudes of the triangle. An altitude is a line that is drawn from a vertex of a triangle and is perpendicular to the opposite side. Therefore, a triangle has three altitudes, one from each vertex. The orthocenter is denoted by H.

The orthocenter has several properties, including:

• The orthocenter is always inside the triangle if the triangle is acute.
• The orthocenter is always outside the triangle if the triangle is obtuse.
• The orthocenter is at the vertex of the right angle if the triangle is right.

The orthocenter can be used to solve a variety of problems involving triangles, such as finding the area of the triangle, finding the length of a side of the triangle, or finding the distance between two points on a side of the triangle.

Here is an example of how to use the orthocenter to find the area of a triangle:

Given: A triangle with vertices A, B, and C.

To find: The area of the triangle.

Solution:

1. Find the orthocenter of the triangle: H

2. Find the altitude from vertex A to side BC: h

3. Find the altitude from vertex B to side AC: k

4. Find the area of the triangle: S = (1/2) * h * k

Therefore, the area of the triangle is S.

Questions for Practice

Here are some questions on Incircle, Inradius, Circumcenter, Circumradius & Orthocenter.

1. If ‘I’ the incentre of triangle ABC such that angle BAC = 44^o, then find the measure of angle BIC.

A) 112^o

B) 68^o

C) 88^o

D) 44^o

2. If the length of three sides of a triangle are 8 cm, 10 cm and 12 cm while the inradius of the triangle is 5 cm, then find the area of the triangle.

 A) 37.5 cm²

B) 150 cm²

C) 75 cm²

D) 300 cm²

3. If ‘M’ is the circum-centre of triangle PQR such that angle QPR = 36^o, then find the measure of angle QMR.

A) 18^o

B) 72^o

C) 108^o

D) 60^o

4. If the length of three sides of a triangle is ‘a’ cm, 12 cm and 15 cm, respectively such that its area is 54 cm², then find the value of given that the length of circum-radius of the triangle is 7.5 cm.

A) 9 cm

B) 4.5 cm

C) 18 cm

D) 10 cm

5. If ‘O’ is the ortho-centre of triangle ABC, such that angle BOC = 50^o, then find the measure of angle BAC.

A) 120^o

B) 100^o

C) 110^o

D) 130^o

1. Ans: A

Solution:

Since, ‘I’ is the in-centre of the circle.

So, angle BIC = 90^o + (1/2) × angle BAC = 90^o + (1/2) × 44^o = 90^o + 22^o = 112^o

2. Ans: C

Solution:

Inradius of a triangle = {area of a triangle/semi perimeter of the triangle}

Since, semi-perimeter of the given triangle = (8 + 12 + 10)/2 = 15 cm

Area of the triangle = (inradius of the triangle) × (semi-perimeter of the triangle) = 15 × 5 = 75 cm²

3. Ans: B

Solution:

Since, ‘M’ is the circumradius of triangle PQR

So, angle QMR = 2 × (angle QPR) = 2 × 36^o = 72^o

4. Ans: A

Solution:

If length of three sides of a triangle are ‘x’ units, ‘y’ units and ‘z’ units, then

Length of circumradius of a triangle = {(x × y × z) ÷ (4 × area of the triangle)}

So, (a × 12 × 15) ÷ (4 × 54) = 7.5

So, a = 9

5. Ans: D

Solution:

Since, ‘O’ is the ortho-centre of the triangle

So, angle BOC = 180^o – angle BAC

So, 50^o = 180^o – angle BAC

So, angle BAC = 180^o – 50^o = 130^o