Mensuration For SSC CGL Exam, Basics & Practice Questions

Mensuration For SSC CGL Exam

Mensuration For SSC CGL Exam: Mensuration is one of the topics that can be asked in many government exams. Candidates can expect at least 2-3 mensuration questions at the difficulty level of easy to moderate in the SSC CGL Exam. Mensuration is a type of topic that belongs to quantitative aptitude and is used in daily life. In this blog, we have provided the basic concept of Mensuration along with the formulas. We have also provided the questions on mensuration in both Hindi and English language along with the answers and their detailed solutions. Candidates are advised to understand the basics first and then try to solve the questions.

Concept of Mensuration

Mensuration is a mathematical concept that deals with the measurement of figures and shapes such as length, width, height, area, perimeter, etc.

Formulas of Mensuration For 2D Shapes:

Rectangle:

• Area of Rectangle = Length × Breadth.
• Perimeter of a Rectangle = 2 × (Length + Breadth)
• Length of the Diagonal = √(Length² + Breadth²)

Square:

• Area of a Square = Length × Length = (Length)² 
• Perimeter of a square = 4 × Length
• Length of the Diagonal = √2 × Length

Parallelogram:

• Area of a Parallelogram = Length × Height
• Perimeter of a Parallelogram = 2 × (Length + Breadth)

Triangle:

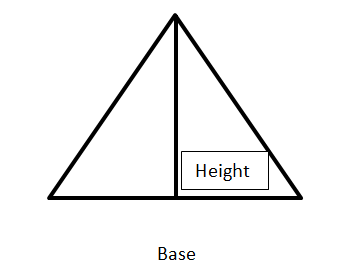
• Area of a triangle=(1/2)(Base × Height)

For a triangle with sides measuring a, b and c, respectively:

• Perimeter = a + b + c
• s = semi perimeter = perimeter/2 =  (a+b+c)/2
• Area of Triangle,

Trapezium:

• Area of a trapezium = (1/2) × (sum of parallel sides) × (distance between parallel sides)
  = (1/2) × (AB+DC) × AE
• Perimeter of a Trapezium = Sum of All Sides

Rhombus:

• Area of a rhombus=(1/2)×Product of diagonals
• Perimeter of a rhombus = 4 × l

Mensuration Formulas For 3D Shapes

Questions on Mensuration with Solutions

Practice the different types of questions related to mensuration and find detailed solutions along with the explanation.

Mensuration Questions in the English Language

Question 1: A solid metallic sphere of radius 26 cm is melted and recast into a cone having diameter of the base as 26 cm. What is the height of the cone?

A) 104 cm

B) 492 cm

C) 416 cm

D) 304 cm

Question 2: How many spheres each of radius 2.1 cm can be formed by melting a metallic cuboid if the length, breadth and height of the cuboid are 44.1 cm, 15 cm and 22 cm, respectively?

A) 380

B) 365

C) 350

D) 375

Question 3: The radius and height of right circular cylindrical pipe are 21 cm and 7 cm. Find the cost of overlaying the curved part of the pipe with aluminium sheet costing Rs. 2 per cm²

A) Rs. 1,848

B) Rs. 422

C) Rs. 844

D) Rs. 924

Question 4: A solid copper sphere of radius 9 cm is melted and moulded into a right circular cylindrical rod of radius 3 cm. What is the length of this rod?

A) 112 cm

B) 108 cm

C) 180 cm

D) 90 cm

Question 5: Base radius of a right circular cone is equal to the edge of a cube whose volume is equal to the 1728 m³. Find the height of the cone if slant height of the cone is 37 metres.

A) 35 metres

B) 37 metres

C) 32 metres

D) 34 metres

Question 6: Base area of a right circular cylinder is equal to the area of a rectangle having its length 6.6 cm. What will be the perimeter of the rectangle if radius of the cylinder is 2.1 cm? (Take π = )

A) 17.4 cm

B) 8.7 cm

C) 14.6 cm

D) 16.8 cm

Question 7: The radii of the ends of a frustum of a cone are 5 cm and 2 cm. Find the volume of frustrum if its height is 14 cm. (Use π = )

A) 548 cm³

B) 572 cm³

C) 458 cm³

D) 624 cm³

Question 8: The length of the edge of a cube is 6.3 cm. What will be the volume of the largest sphere that can be carved out from the cube? (Take π = )

A) 156.328 cm³

B) 130.977 cm³

C) 160.321 cm³

D) 172.324 cm³

Question 9: A rectangular water tank is 3 metres high, 6 metres long and 7 metres wide. How much water (in litres) can it hold?

A) 1,26,000

B) 1,44,000

C) 1,14,000

D) 1,26,00

Mensuration Questions in the Hindi Language

प्रश्न 1: 26cm त्रिज्या वाले एक ठोस धातु के गोले को पिघलाकर 26cm आधार व्यास वाले एक शंकु में बदल दिया जाता है। शंकु की ऊंचाई कितनी है?

A) 104 cm

B) 492 cm

C) 416 cm

D) 304 cm

प्रश्न 2: यदि घनाभ की लंबाई, चौड़ाई और ऊंचाई क्रमशः 44.1cm , 15cm और 22cm है, तो एक धात्विक घनाभ को पिघलाकर 2.1cm त्रिज्या वाले कितने गोले बनाए जा सकते हैं?

A) 380

B) 365

C) 350

D) 375

प्रश्न 3: लंब वृत्ताकार बेलनाकार पाइप की त्रिज्या और ऊँचाई 21cm और 7cm है। पाइप के वक्र हिस्से को Rs. 2 per cm² की दर से एल्यूमीनियम शीट से ढकने की लागत ज्ञात कीजिए।

A) Rs. 1,848

B) Rs. 422

C) Rs. 844

D) Rs. 924

प्रश्न 4: 9cm त्रिज्या वाले एक ठोस तांबे के गोले को पिघलाकर 3cm त्रिज्या वाली एक लंब वृत्ताकार बेलनाकार छड़ में ढाला जाता है। इस छड़ की लंबाई कितनी है?

A) 112 cm

B) 108 cm

C) 180 cm

D) 90 cm

प्रश्न 5: एक लंब वृत्तीय शंकु के आधार की त्रिज्या एक घन के किनारे के बराबर है जिसका आयतन 1728 m³ के बराबर है। यदि शंकु की तिरछी ऊंचाई 37 metres है तो शंकु की ऊंचाई ज्ञात करें।

A) 35 metres

B) 37 metres

C) 32 metres

D) 34 metres

प्रश्न 6: एक लम्ब वृत्तीय बेलन का आधार क्षेत्रफल, एक आयत के क्षेत्रफल के बराबर है जिसकी लंबाई 6.6 cm है। यदि बेलन की त्रिज्या 2.1 cm है तो आयत का परिमाप क्या होगा? (π = लें)

A) 17.4 cm

B) 8.7 cm

C) 14.6 cm

D) 16.8 cm

प्रश्न 7: एक शंकु के छिन्नक के सिरों की त्रिज्याएँ 5 cm और 2 cm हैं। यदि छिन्नक की ऊँचाई 14 cm है तो उसका आयतन ज्ञात करें। (π = का प्रयोग करें)

A) 548 cm³

B) 572 cm³

C) 458 cm³

D) 624 cm³

प्रश्न 8: एक घन के किनारे की लंबाई 6.3 cm है। घन से निकाले जा सकने वाले सबसे बड़े गोले का आयतन क्या होगा? (Take π = )

A) 156.328 cm³

B) 130.977 cm³

C) 160.321 cm³

D) 172.324 cm³

प्रश्न 9: एक आयताकार पानी टैंक 3 metres ऊंची, 6 metres लंबी और 7 metres चौड़ी है। इसमें कितना पानी (litres में) आ सकता है?

A) 1,26,000

B) 1,44,000

C) 1,14,000

D) 1,26,00

ANSWER KEYS and SOLUTIONS:

Solutions of the Above Questions with Explanation

Solution 1: 3)

Since we know volume of a sphere = 4/3πr³ and volume of a cone = 1/3πr²h

Here r = radius, h = height

Let the height of the cone be ‘h’

Radius of the base of the cone = (26/2) = 13 cm

Now,

(4/3) X π X 26³ = (1/3) X π X 13² X h

Or, 4 X 17576 = 169 X h

So, h = 416

So, height of the cone = 416 cm

Hence, option c.

Solution 2: 4)

Let the number of spheres that can be formed be ‘n’.

ATQ, volume of cuboid = volume of ‘n’ spheres

So, 44.1 X 15 X 22 = n x (4/3) x (22/7) x (2.1)³

So, ‘n’ = 375

Hence, option d.

Solution 3: 1)

We know, curved surface area of a cylinder = 2π X Radius of cylinder X Height of cylinder

Or, curved surface area of the given pipe = 2 X (22/7) X 7 X 21 = 924 cm²

Required cost of overlaying = 924 X 2 = Rs. 1,848

Hence, option a.

Solution 4: 2)

Since, the sphere is moulded in form of the cylindrical rod, therefore their volumes will be equal

Let the length/height of the rod be ‘h’ cm

ATQ:

Since we know volume of a sphere = (4/3) x π x radius³

And we also know volume of a cylinder = π X radius² X length

Or, 4 X 243 = 9 X ‘h’

Or, ‘h’ = 108

So, length of the rod = 108 cm

Hence, option b.

Solution 5: 1)

Let the height of the cone be ‘h’ metres.

ATQ,

volume of the cube = 1728

Or, edge³ = 1728

So, edge of the cube = 12 metres

radius of the cone (r) = edge of the cube = 12 metres

Since, slant height² = height² + radius²

So, ‘h’ = 

Or, ‘h’ = 

Or, ‘h’ = 

So, ‘h’ = 35

Required height = 35 metres

Hence, option a.

Solution 6: 1)

Let the breadth of the rectangle be ‘b’ cm and radius of the c

ATQ, πr² = 6.6 X b

Or, 

Or, ‘b’ = 

So, ‘b’ = 2.1

So, perimeter of the rectangle = 2 X (length + breadth)

= 2 X (6.6 + 2.1)

= 2 X 8.7

= 17.4 cm

Hence, option a.

Solution 7: 2)

Volume of a frustum of a cone = (πh/3) X (R² + r² + Rr)

(Where ‘R’ = larger radius, ‘r’ = smaller radius and ‘h’ = height of the cone)

So, volume = (1/3) X (22/7) X 14 X (5² + 2² + 5 X 2)

= (44/3) X (25 + 4 + 10)

= (44/3) X 39

= 572 cm³

Hence, option b.

Solution 8: 2)

Let the radius of the sphere be ‘r’ cm.

For maximum volume of the sphere, diameter of the sphere will be equal to the length of the edge of the cube.

So, radius of the sphere = (6.3/2) cm

So, Required volume = (4π/3) x r³ =(4/3) x (22/7) x (6.3/2) X (6.3/2) X (6.3/2) = 130.977 cm³

Hence, option b.

Solution 9: 1)

As we know, volume of a cuboid = Length X Breadth X Height

So, volume of the tank = 3 X 6 X 7 = 126 m³

1 m³ = 1000 litres

So, quantity of water the tank can hold = 126 X 1000 = 1,26,000 litres

Hence, option a.

Mensuration For SSC CGL Exam FAQs

• Sign Up on Practicemock for Updated Current Affairs, Free Topic Tests and Free Mini Mocks
• Sign Up Here to Download Free Study Material