GATE, a rigorous engineering competitive exam, stands as a crucial challenge in the realm of engineering. Aspirants eyeing M.Tech courses in esteemed engineering institutions center their preparation on this examination. To excel in GATE, candidates must possess a profound understanding of the GATE 2024 exam pattern to secure top-notch scores.
The GATE exam pattern for 2024, released by IISc Bangalore, serves as a valuable guide for aspiring students. Following this pattern enables students to prepare thoroughly and enhance their chances of securing impressive marks in the GATE Exam.
It is imperative to be mindful of the recurring question types in the exam to successfully crack it. To facilitate this understanding, we offer the GATE Previous Year Paper PDF with Detailed Solutions, providing insight into the SBI Clerk prelims 2023 examination’s difficulty level. Before delving into the GATE previous year paper PDF, let’s take a swift look at the GATE exam pattern for Civil Engineering and Mechanical Engineering.
GATE 2024 Exam Pattern for Civil Engineering
Dive into the specifics of Engineering Mathematics, General Aptitude, and Civil Engineering subjects, with question numbers, marks, and subject-wise breakdown provided in the following table:
| Subject | No. of Questions | Marks |
| Engineering Mathematics | 10 | 13 |
| General aptitude | 10 | 15 |
| Civil engineering subject | 45 | 72 |
| Total | 65 | 100 |
Examining the GATE CE Exam Pattern from the Past: After exploring the previous year’s exam, we can say that the type of questions that come in the exam are as follows:
- Application & Formula Based
- Questions Based on Core Topics
- Figures Based Questions
- Questions Based on Analysis or Common Data Questions
- Linked Questions
GATE 2024 Exam Pattern for Mechanical Engineering
Gain insight into the Mechanical Engineering exam pattern for GATE 2024, a crucial aspect for comprehensive preparation. This branch witnesses the highest number of GATE aspirants, and key details are outlined below:
| Aspects | Details |
| Total Marks | 100 |
| Total no. of Questions | 65 |
| Exam Duration | 3 hours |
| General Aptitude Weightage | 15% of Total Marks |
| Engineering Mathematics Weightage | 13% of Total Marks |
| Mechanical Engineering Weightage | 72% of Total Marks |
GATE CE 2022 Previous Year Paper-Slot 1
Questions 1 to 5 carry ONE mark each.
Q1. You should _________ when to say ________.
(1) no/no
(2) no / know
(3) know/know
(4) know/no
Answer key: 4
Solution:
For the first blank, we need a base form verb to follow the modal SHOULD, and for the second blank, we need an interjection. KNOW (be aware of) will fit in the first blank, and NO (used to indicate a negative response) will fit in the second blank. The sentence tells us how one must be aware of when one must refuse. Thus, D is the right answer.
Q2. Two straight lines pass through the origin (xo, yo) = (0,0). One of them passes through the point (x1, y1) = (1, 3) and the other passes through the point ((x2, y2) = (1, 2).
What is the area (in square units) enclosed between the straight lines in the interval [0, 1] on the x – axis?
(1) 0.5
(2) 1.0
(3) 1.5
(4) 2.0
Answer key: 1
Solution:
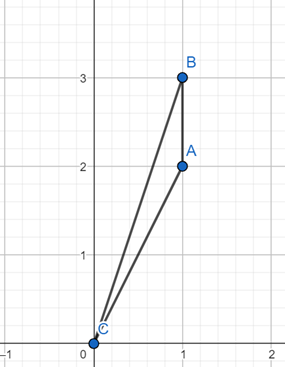
Required area = Area of triangle ABC
Area of triangle = (1/2) × base × Height
So, area of triangle ABC = (1/2) × AB × height of the triangle
AB = 1 units and height of the triangle = 1 unit
So, required area = (1/2) × 1 × 1 = 0.5 square units
Hence, option a.
Q3. If p:q = 1:2, q:r = 4:3 and r:s = 4:5 and ‘u’ is 50% more than ‘s’, then what is the ratio p:u?
(1) 2:15
(2) 16:15
(3) 1:5
(4) 16:45
Answer key: 4
Solution:
Let p = ‘12x’
So, q = 12x × (2/1) = ‘24x’
And ‘r’ = 24x × (3/4) = ‘18x’
And ‘s’ = 18x × (5/4) = ‘22.5x’
So, ‘u’ = 22.5x × (3/2) = ‘33.75x’
So, required ratio = 12x: 33.75x = 16 : 45
Hence, option d.
Q4. Given the statements:
P is the sister of Q.
Q is the husband of R.
R is the mother of S.
T is the husband of P.
Based on the above information, T is _______ of S.
(1) the grandfather
(2) an uncle
(3) the father
(4) a brother
Answer key: 2
Solution:
Clues:
1) P is the sister of Q.
2) Q is the husband of R.
3) R is the mother of S.
4) T is the husband of P.
Inferences:
From clue 1 and 2, P is sister of Q, who is husband of R.
From clue 3 and 4, S is either son or daughter of Q. T is husband of P.
We draw the following Blood relation:
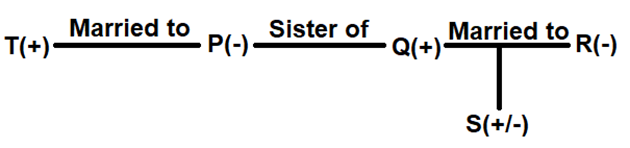
T is an uncle of S.
Hence, option b.
Q5. In the following diagram, the point R is the center of the circle. The lines PQ and ZV are tangential to the circle. The relation among the areas of the squares, PXWR, RUVZ and SPQT is
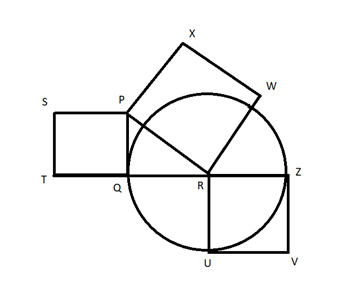
(1) Area of SPQT = Area of RUVZ = Area of PXWR
(2) Area of SPQT = Area of PXWR – Area of RUVZ
(3) Area of PXWR = Area of SPQT – Area of RUVZ
(4) Area of PXWR = Area of RUVZ – Area of SPQT
Answer key: 2
Solution:
Let ‘QR’ = ‘r’ cm
So, area of square RUVZ = r2 (As QR = RU = radius of the circle)
And ‘PR’ = ‘a’ cm
And area of square PXWR = a2
Since, PQ is tangent of the given circle, ∠PQR = 90o
So, PQR is a right-angled triangle.
And Length of PQ = √(a2 – r2)
So, area of square SPQT = {√(a2 – r2)}2 = a2 – r2
So, Area of SPQT = Area of PXWR – Area of RUVZ
Hence, option b.
Questions 6 to 10 carry TWO marks each.
Q6. Healthy eating is a critical component of healthy aging. When should one start eating healthy? It turns out that it is never too early. For example, babies who start eating healthy in the first year are more likely to have better overall health as they get older.
Which one of the following is the CORRECT logical inference based on the information in the passage?
(1) Healthy eating is important for those with good health conditions, but not for others
(2) Eating healthy can be started at any age, earlier the better
(3) Eating healthy and better overall health are more correlated at a young age, but not older
(4) Healthy eating is more important for adults than kids
Answer key: 2
Solution:
The given text tells us how it is never too early to start eating healthy. It also gives an example of babies who start eating healthy in the first year, and how they have better overall health as they get older. From this, we can conclude that eating healthy can be begun at any age, but the earlier one does, the better it is. Thus, B is the right answer.
A is incorrect as the passage does not talk about people with health conditions. C and D cannot be concluded from the text.
Q7. ‘P’ invested ₹ 5,000 per month for 6 months of year and ‘Q’ invested ₹’x’ per month for 8 months of the year in a partnership business. The profit is shared in proportion to the total investment made in that year. If at the end of that investment year, ‘Q’ receives of the total profit, what is the value of ‘x’?
(1) 2500
(2) 3000
(3) 4687
(4) 8437
Answer key: 2
Solution:
Ratio of profit shares of ‘P’ and ‘Q’ at the end of the year = 5:4
ATQ;
{(5000 × 6)/(x × 8)} = (5/4)
Or, 120000 = 40x
So, x = 3000
Hence, option b.
Q8. The frequency chart given below shows the frequency distribution of marks obtained by a set of students in an exam.
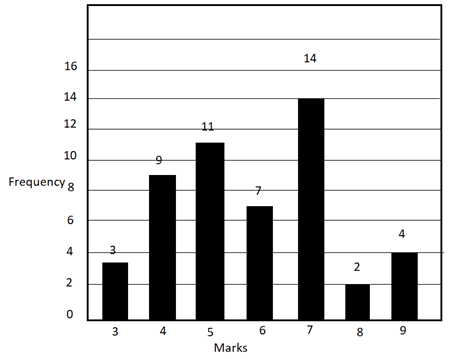
From the data presented above, which one of the following is CORRECT?
(1) Mean > mode > median
(2) Mode > median > mean
(3) Mode > mean > median
(4) Median > mode > mean
Answer key: 2
Solution:
Mean = Sum of observations ÷ Total number of observations
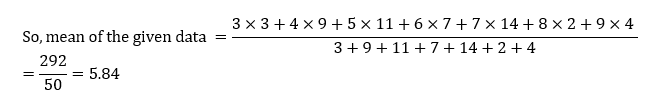
Total number of observations = 50
So, median = mean of (50/2)th and (50/2 + 1)th term
So, median term = mean of 25th and 26th term.
Here both 25th and 26th term are 6.
So, median = (6 + 6)/2 = 6
And mode = Marks obtained by maximum students i.e., 7
So, mode > median > mean
Hence, option b.
Q9. In the square grid shown on the left, a person standing at P2 position is required to move to P5 position.
The only movement allowed for a step involves, “two moves along one direction followed by one move in a perpendicular direction”. The permissible directions for movement are shown as dotted arrows in the right.
For example, a person at a given position Y can move only to the positions marked X on the right.
Without occupying any of the shaded squares at the end of each step, the minimum number of steps required to go from P2 to P5 is
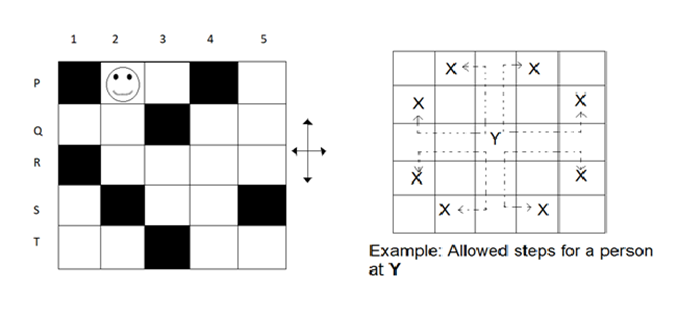
(1) 4
(2) 5
(3) 6
(4) 7
Answer key: 2
Solution:
Here, as it is given that person will move ‘two moves along one direction followed by one move in a perpendicular direction’. And he/she cannot occupy the shaded portion but they can go through the shaded portion.
Minimum step required to go from P2 to P5 is:
First, he moves from P2 to Q4, then from Q4 to S3, then from S3 to T5, then from T5 to R4 and at last from R4 to P5.
So, the minimum number of steps required is ‘5’
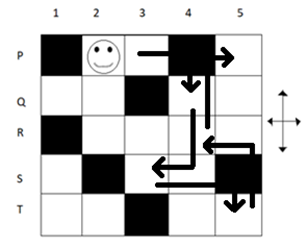
So, the minimum number of steps required is ‘5’
Hence, option b.
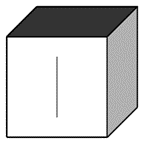
Q10. Consider a cube made by folding a single sheet of paper of appropriate shape. The interior faces of the cube are all blank and the exterior faces that are not visible are also blank.
Which one of the following represents a possible unfolding of the cube?
(1)
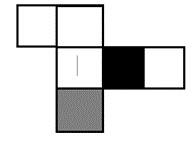
(2)
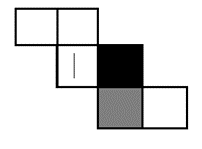
(3)
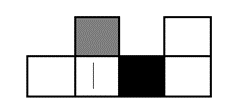
(4)
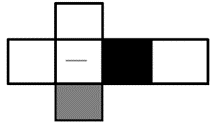
Answer key: 4
Solution:
This question in the paper was wrong. So, we have made some changes to the question to make it correct.
Here, we see that the straight line is perpendicular to the black portion and parallel to the grey portion of the dice. So, by this we can eliminate option ‘a’, ‘b’ and ‘c’.
GATE CE 2022 Previous Year Paper-Slot 2
Questions 1 to 5 carry ONE mark each.
- The movie was funny and I _______.
(1) Could help laughing
(2) Couldn’t help laughed
(3) Couldn’t help laughing
(4) Could helped laughed
Answer key: 3
Solution:
We need a verb clause to agree with the subject pronoun I. COULDN”T HELP LAUGHING means to be unable to control one’s laughter, and will fit here as the sentence tells us how the movie was funny and made the speaker laugh. Thus, C is the right answer.
A, B and D are incorrect as the correct phrase is Couldn’t + Help + Present participle (doing something).

(1) 0.75
(2) 1.25
(3) 2.25
(4) 3.25
Answer key: 2
Solution:
Let ‘x’ = ‘12a’ {LCM (2, 3 and 4)}
So, ‘y’ = 12a ÷ (1/2) × (1/3) = ‘8a’
And ‘z’ = 12a ÷ (1/2) × (1/4) = ‘6a’
So, required value = (12a + 6a – 8a) ÷ 8a = ‘1.25’
Hence, option b.
- Both the numerator and the denominator of fraction
are increased by a positive integer, ‘x’, and those of fraction
are decreased by the integer ‘x’. This operation results in the same value for both the fractions. What is the value of ‘x’?
(1) 1
(2) 2
(3) 3
(4) 4
Answer key: 3
Solution:
ATQ;
{(3 + x)/(4 + x)} = {(15 – x)/(17 – x)}
Or, (17 – x)(3 + x) = (15 – x)(4 + x)
Or, 51 – 3x + 17x – x2 = 60 + 15x – 4x – x2
Or, 14x – 11x = 9
Or, 3x = 9
So, x = 3
Hence, option c.
Download More Question-Complete PDF from here
GATE ME 2022 Previous Year Paper-Slot 1
Questions 1 to 5 carry ONE mark each.
- The average monthly salaries of M, N and S is ₹ 4000. The average of the monthly salaries of N, S and P is ₹ 5000. The monthly salary of P is ₹ 6000. What is the monthly salary of M as a percentage of the monthly salary of P?
(1) 50%
(2) 75%
(3) 100%
(4) 125%
Answer key: 1
Solution:
Given,
Average of the monthly salaries of M, N, S = 4000 Rs
Average of monthly salaries of N, S, P = 5000 Rs
Monthly salary of P = 6000 Rs
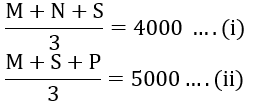
From equation (i) and (ii)
N + S = 12000 – M
N + S = 15000 – P
12000 – M = 15000 – P
12000 – M = 15000 – 6000
M = 3000 Rs

2. After playing _______ hours of tennis, I am feeling_______ tired to walk back.
(1) too/too
(2) too/two
(3) two/two
(4) two/too
Answer key: 4
Solution:
After playing two hours of tennis, I am feeling too tired to walk back.
3. A person travelled 80 km in 6 hours. If the person travelled the first part with a uniform speed of 10 kmph and the remaining part with a uniform speed of 18 kmph. What percentage of the total distance is travelled at a uniform speed of 10 kmph?
(1) 28.25
(2) 37.25
(3) 43.75
(4) 50.00
Answer key: 3
Solution:
Given,
Total distance D1 + D2 = 80 km, Total time taken t1 + t2 = 6 hours
First part with a uniform speed = 10 kmph
So, D1= 10 × T1
Remaining part with a uniform speed of 18 kmph
So, D1 = 18 × t2
as D1 + D2 = 80
10 t1 + 18 t2 = 80
10 t1 + 18 (6 –t1) = 80
t1 = hours
4. Four girls P, Q, R and S are studying languages in a University. P is learning French and Dutch. Q is learning Chinese and Japanese. R is learning Spanish and French. S is learning Dutch and Japanese.
Given that: French is easier than Dutch; Chinese is harder than Japanese; Dutch is easier than Japanese, and Spanish is easier than French.
Based on the above information, which girl is learning the most difficult pair of languages?
(1) P
(2) Q
(3) R
(4) S
Answer key: 2
Solution:
Languages as per difficulty are arranged as: Chines > Japanese > Dutch > French > Spanish Since Q is learning Chinese and Japanese, Q is learning most difficult pair of language.
5. A block with a trapezoidal cross-section is placed over a block with a rectangular cross-section as shown above.
1.
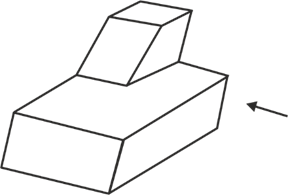
Which one of the following is the correct drawing of the view of the 3D object as viewed in the direction indicated by an arrow in the above figure?
(1)

(2)

(3)

(4)

Answer key: 1
Solution:

This is the correct drawing of the view of the 3D object as viewed in the direction indicated by an arrow in the above figure.
GATE ME 2022 Previous Year Paper-Slot 2
Questions 1 to 5 carry ONE mark each.
- Writing too many things on the ________ while teaching could make the students get _________.
(1) bored / board
(2) board / bored
(3) board / board
(4) bored / bored
Answer key: 2
Solution:
For the first blank, we need a noun to be modified by the definite article THE, and for the second blank, we need an adjective to modify the noun STUDENTS. The sentence tells us how writing too much on the blackboard while teaching can kill the interest of the students. BOARD (referring to the blackboard) will fit in the first blank, and BORED (uninterested) will fit in the second blank. Thus, B is the right answer.
2. Which one of the following is a representation (not to scale and in bold) of all values of ‘x’ satisfying the inequality:
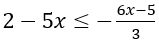
on the real number line?
(1)
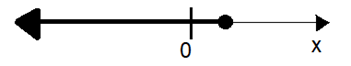
(2)
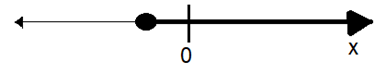
(3)

(4)

Answer key: 3
Solution:
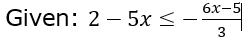
= 6 – 15x ≤ 5 – 6x
= 1 ≤ 9x
So, x ≥ (1/9)
Among the given options, only ‘C’ shows the graph where x ≥ (1/9).
Hence, option c.
3.

(1) (1/2)
(2) 1
(3) 2
(4) 4
Answer key: 3
Solution:
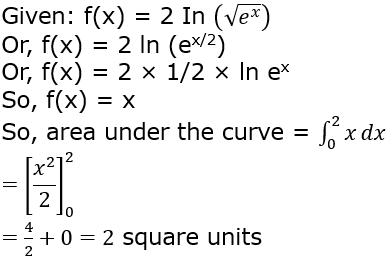
Or, f(x) = 2 ln (ex/2)
Or, f(x) = 2 × 1/2 × ln ex
So, f(x) = x

Hence, option b.
4. A person was born on the fifth Monday of February in a particular year. Which one of the following statements is correct based on the above information?
(1) The 2nd February of that year is a Tuesday
(2) There will be five Sundays in the month of February in that year
(3) The 1st February of that year is a Sunday
(4) All Mondays of February in that year have even dates
Answer key: 1
Solution:
If a person was born on the fifth Monday of February in a particular year then the only possibility is that the person must be born on a leap year.
| February | |||||
| Sunday | 7 | 14 | 21 | 28 | |
| Monday | 1 | 8 | 15 | 22 | 29 |
| Tuesday | 2 | 9 | 16 | 23 | |
| Wednesday | 3 | 10 | 17 | 24 | |
| Thursday | 4 | 11 | 18 | 25 | |
| Friday | 5 | 12 | 19 | 26 | |
| Saturday | 6 | 13 | 20 | 27 | |
Among the given options, only option ‘a’ is correct.
There are only four Sundays in the month of February in that year, the 1st February of that year is Monday and only the 2nd and the 4th Monday have even dates.
Hence, option a.
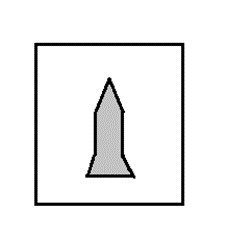
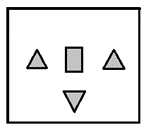
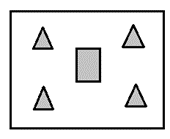
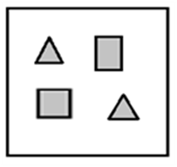
Which one of the groups given below can be assembled to get the shape that is shown above using each piece only once without overlapping with each other? (rotation and translation operations may be used).
(1)
(2)
(3)
(4)
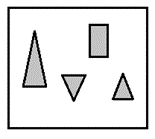
Answer key: 2
Solution:
Note: There were two correct options in the actual exam, option ‘b’ and option ‘c’. However option ‘c’ has been modified in this particular question.
The groups which can be assembled to get the shape that is shown above using each piece only once without overlapping with each other (rotation and translation operations may be used) is as follows:
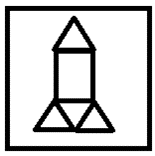
Hence, option b.
- Sign Up on Practicemock for Updated Current Affairs, Free Topic Tests and Free Mini Mocks
- Sign Up Here to Download Free Study Material
Free Mock Tests for the Upcoming Exams
- IBPS PO Free Mock Test
- RBI Grade B Free Mock Test
- IBPS SO Free Mock Test
- NABARD Grade A Free Mock Test
- SSC CGL Free Mock Test
- IBPS Clerk Free Mock Test
- IBPS RRB PO Free Mock Test
- IBPS RRB Clerk Free Mock Test
- RRB NTPC Free Mock Test
- SSC MTS Free Mock Test
- SSC Strenographer Free Mock Test
- GATE Mechanical Free Mock Test
- GATE Civil Free Mock Test
- RRB ALP Free Mock Test
- SSC CPO Free Mock Test
- AFCAT Free Mock Test
- SEBI Grade A Free Mock Test
- IFSCA Grade A Free Mock Test
- RRB JE Free Mock Test
- Free Banking Live Test
- Free SSC Live Test





